If you’ve been writing software for very long, you’ve likely encountered the humble ring buffer. Ring buffers are everywhere . They appear in code for audio engines, network stacks, kernel drivers, graphics engines, etc. They’re one of the most important data structures for getting data from point A to point B in a timely and thread-safe way. Today, we’re going to show the ring buffer some love. We’ll talk about how the ring buffer works, why you might use it, and we’ll even implement one in C++.
What Is a Ring Buffer?
You may have heard of something called a circular buffer, or maybe even a cyclic queue. Both of those are just other names for the ring buffer. You can think of a ring buffer as a specialized type of queue. Just as with any old, vanilla queue, a producer produces some data, shoves it into the data structure, and a consumer comes along and consumes it. This all happens in first-in-first-out (FIFO) order. But what sets the ring buffer apart is the way it manages its data and the limitations it imposes.
A ring buffer has a fixed capacity. It can’t grow and it can’t shrink. If you create a ring buffer that can store 10 items, 10 items will forever be its max capacity. Because the capacity is fixed, a producer has two options once it fills the ring buffer – the choice of which is largely driven by how the ring buffer is designed and the application’s needs. The producer can either wait until a slot is free in the ring buffer so that it can add more data. Or it can just stomp over data that hasn’t been consumed yet. Both approaches are valid in certain contexts.
The consumer’s role is to consume data. If there’s no data available in the ring buffer, the consumer has to wait or go do something else. The side-effect of a consumer reading data is that it frees up slots within the ring buffer for the producer to use.
Ideally, the producer’s producing is always just slightly ahead of the consumer’s consuming, resulting in a nice game of “catch me if you can” with virtually no waiting by either party.
The canonical diagram of a ring buffer looks like so.
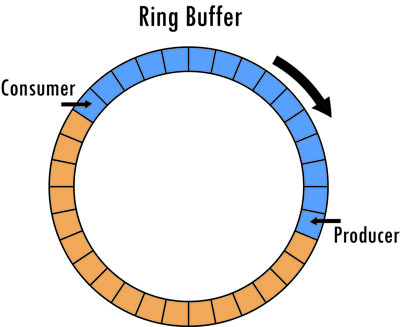
In this diagram, we have a buffer with 32 slots. The producer has filled 15 of them, indicated by blue. The consumer is behind the producer, reading data from the slots, freeing them as it does so. A free slot is indicated by orange.
Keep in mind that these sorts of diagrams are meant to demonstrate a concept and not so much depict an implementation. It’s certainly possible to implement a ring buffer that’s physically circular, as in the image above, using something like a linked list of separate smaller buffers. Quite often, however, you’ll see a ring buffer implemented using one big memory allocation. In this case, separate state is used to track used capacity as well as read and write indices.
Why Use a Ring Buffer?
You’ll most commonly see ring buffers used in circumstances that involve high volumes of data that need to be produced and consumed at high speeds. Real-time audio/video, network drivers, etc. are all contexts where you’ll find ring buffers being used. In these situations, performance of the data structure is key.
Performance takes a beating if you’re having to allocate and deallocate memory all the time. Memory allocation is slow. So ring buffers avoid it by allocating a chunk of memory one time and reusing it over and over. Memory fragmentation is also avoided.
Anything that involves locking (e.g., mutexes, and even memory allocation) is problematic when it comes to performance. You simply can’t predict how long a lock will be held. As we’ll see in our example implementation, ring buffers can be both thread-safe and lock-free.
Speed Is My Jam. When Would I Not Want to Use a Ring Buffer?
Ring buffers are ideally suited for the single producer/single consumer scenario. If there are more than one of either, things get complicated and locking will certainly need to be introduced either directly within the ring buffer or as a wrapper.
If you need your data structure to grow to an arbitrary size, then ring buffers are off the table.
If you need to explicitly control the lifetime of data within the ring buffer (e.g., if you need to hold pointers/references to contained data), then ring buffers are obviously the wrong choice.
If your data needs to be sorted or have a priority associated with it, ring buffers are the wrong choice here as well. Ring buffers are ALWAYS first-in, first-out.
The Gotcha
Because the ring buffer size is fixed, you sometimes have to experiment to find the optimum size to keep the producer ahead of the consumer at a rate that neither ever has to wait to do their job. Take the world of professional audio software as an example. Here, you’ll sometimes find the ring buffer capacity explicitly configurable within the UI as a mechanism for the user to tradeoff between audio latency and glitchy audio for a given hardware configuration.

When is it ok for a producer to stomp over unconsumed data?
I mentioned earlier that in some scenarios it’s ok for a producer to stomp over unread data. When would this ever be ok? Consider a real-time audio or video streaming application such as a radio streamer or video conferencing app, or perhaps the broadcasting of player states in an online game. For sundry reasons, network hiccups occur. We’ve all experienced them. But regardless of the why, it’s always important to charge forward and have our applications processing the latest and greatest data.
Implementing an Audio Ring Buffer
The time has come. We’re going to implement a simple ring buffer in C++. We’ll make it data type agnostic and lock-free. Let’s start things off with a class skeleton, a constructor that allocates the buffer, and some state for tracking how much of the buffer is free.
template<typename DataType> class RingBuffer { public: RingBuffer(int capacity) : m_capacity(capacity), m_freeItems(capacity), { static_assert(ATOMIC_INT_LOCK_FREE == 2); m_spBuffer = std::make_unique<DataType[]>(m_capacity); memset(m_spBuffer.get(), 0, sizeof(DataType) * m_capacity); } ... private: ... std::unique_ptr<DataType[]> m_spBuffer; const int m_capacity; std::atomic<int> m_freeItems; }; |
This is a data type agnostic implementation. RingBuffer is a class template that allows clients to parameterize it with whatever data type they wish (so long as it’s memcpy and memcmp compatible).
The constructor allows the client to specify the size of the ring buffer. This is stored in m_capacity.
We also have a std::atomic<int> that’s used to track how many free slots are available for writing. Having this atomic is key to making this class thread-safe, as both producers and consumers will be indirectly checking this value during the reading and writing of ring buffer data.
You’ll also note that the constructor has a static_assert for ensuring that std::atomic<int> is lock free. This is to avoid any locking that could impact performance.
And just for fun, we initialize the contents of m_spBuffer to zero to put us in a known initial state. This isn’t really all that important. But it might benefit unit tests (which I did write for this, incidentally).
Next up, let’s add the state and functions needed for writing data into the buffer.
int m_writeIndex; // Initialized to zero in constructor. Not shown above. int getWriteableItemCount() const { return m_freeItems.load(); } int write(DataType * pData, int numItems) { int writeableItemCount = getWriteableItemCount(); if (writeableItemCount == 0) return 0; int totalItemsToWrite = std::min(writeableItemCount, numItems); // Note that writeableItemCount will do nothing to help us // determine if we're on the edge of the buffer and need to wrap around. // That's up to us to determine here. int itemsLeftToWrite = totalItemsToWrite; // Note that we're treating m_capacity like an index here for // one-past-the-end. if ((m_writeIndex + itemsLeftToWrite) >= m_capacity) { // We'd exceed the extent of the buffer here if wrote totalItemsToWrite samples, // so let's do a partial write. int itemsAvailableUntilEnd = m_capacity - m_writeIndex; memcpy(m_spBuffer.get() + m_writeIndex, pData, itemsAvailableUntilEnd); // Bookkeeping m_writeIndex = 0; itemsLeftToWrite -= itemsAvailableUntilEnd; pData += itemsAvailableUntilEnd; } if (itemsLeftToWrite > 0) { memcpy(m_spBuffer.get() + m_writeIndex, pData, itemsLeftToWrite * sizeof(DataType)); // Bookkeeping m_writeIndex += itemsLeftToWrite; itemsLeftToWrite = 0; } m_freeItems -= totalItemsToWrite; return totalItemsToWrite; } |
There’s one new piece of state here and two new functions.
The new state, m_writeIndex, is used to track where the producer is writing next. This value is only ever used by the producer, so we don’t need to make it atomic.
The function getWriteableCount() merely returns the number of free slots available for writing in the ring buffer. It’s for the benefit of both the producer and the write() function itself.
The write() function attempts to write the specified number of items into the ring buffer and returns the actual number of items written. There are some things worth noting here.
We first check to see if we CAN actually write anything. If we can’t, we return immediately.
Next, we decide how MUCH we can actually write and store it in a local variable called totalItemsToWrite. This value may be less than what the producer requested if they requested more than we have space for. After that, we check to see if we might be trying to write more towards the end of the buffer than we have space for. If so, we write what we can and then loop back around to the beginning to write what’s left. Anything that’s left goes wherever the current write position is located.
Before leaving the function, we update the relevant member variables.
Now let’s look at the state and functions for reading data from the buffer.
int m_readIndex; // Initialized to zero in constructor. Not shown above. int getReadableItemCount() const { return m_capacity - m_freeItems.load(); } int read(DataType * pData, int numItems) { int readableItemCount = getReadableItemCount(); if (readableItemCount == 0) return 0; int totalItemsToRead = std::min(readableItemCount, numItems); // Note that readableItemCount will do nothing to help us // determine if we're on the edge of the buffer and need to wrap around. // That's up to us to determine here. int itemsLeftToRead = totalItemsToRead; if ((m_readIndex + itemsLeftToRead) >= m_capacity) { // We'd exceed the extent of the buffer here if read totalItemsToRead items, // so let's do a partial read. int itemsAvailableUntilEnd = m_capacity - m_readIndex; memcpy(pData, m_spBuffer.get() + m_readIndex, itemsAvailableUntilEnd); // Bookkeeping m_readIndex = 0; itemsLeftToRead -= itemsAvailableUntilEnd; pData += itemsAvailableUntilEnd; } if (itemsLeftToRead > 0) { memcpy(pData, m_spBuffer.get() + m_readIndex, itemsLeftToRead * sizeof(DataType)); // Bookkeeping m_readIndex += itemsLeftToRead; itemsLeftToRead = 0; } m_freeItems += totalItemsToRead; return totalItemsToRead; } |
Much like the writing side of things, we have a new piece of state for tracking the consumer’s read position. We also have a complementary getReadItemCount() function for returning the number of items available for reading. And then there’s the read() function.
If you compare the write() and the read() function implementations here, you’ll see they’re almost exactly the same. There are only two big differences – the direction the data goes in and out of m_spBuffer and the way the member variables are updated (m_freeItems being incremented vs. decremented, and m_readIndex being used vs. m_writeIndex). Apart from that, they’re pretty much the same.
The checks against m_freeItems ensure that the consumer will never overtake the producer. And, in this implementation, the producer can never overwrite data. So accessing m_spBuffer from two different threads is safe because the producer and consumer are never accessing the same slots at the same time.
The only other shared state between the producer and the consumer is m_freeItems and that’s atomic.
The complete RingBuffer implementation is as follows.
/** * A simple ring buffer class. This is thread-safe so long as only a * single producer and a single consumer are clients. */ template<typename DataType> class RingBuffer { public: /** * Constructor. * * @param capacity The total number of items to accommodate in the RingBuffer. */ RingBuffer(int capacity) : m_capacity(capacity), m_freeItems(capacity), m_readIndex(0), m_writeIndex(0) { // Lock-free would be important for scenarios that can't use locking, such // as real-time audio. If you don't have real-time concerns, then this can // possibly be removed. static_assert(ATOMIC_INT_LOCK_FREE == 2); m_spBuffer = std::make_unique<DataType[]>(m_capacity); memset(m_spBuffer.get(), 0, sizeof(DataType) * m_capacity); } /** * @return The number of items that can be read by the consumer. */ int getReadableItemCount() const { return m_capacity - m_freeItems.load(); } /** * @return The number of items that can be written by the producer. */ int getWriteableItemCount() const { return m_freeItems.load(); } /** * Attempts to read the specified number of items. * * @return The number of items read. */ int read(DataType * pData, int numItems) { int readableItemCount = getReadableItemCount(); if (readableItemCount == 0) return 0; int totalItemsToRead = std::min(readableItemCount, numItems); // Note that readableItemCount will do nothing to help us // determine if we're on the edge of the buffer and need to wrap around. // That's up to us to determine here. int itemsLeftToRead = totalItemsToRead; // Note that we're treating m_capacity like an index here for // one-past-the-end. if ((m_readIndex + itemsLeftToRead) >= m_capacity) { // We'd exceed the extent of the buffer here if we read totalItemsToRead // items, so let's do a partial read instead. int itemsAvailableUntilEnd = m_capacity - m_readIndex; memcpy(pData, m_spBuffer.get() + m_readIndex, itemsAvailableUntilEnd); // Bookkeeping m_readIndex = 0; itemsLeftToRead -= itemsAvailableUntilEnd; pData += itemsAvailableUntilEnd; } if (itemsLeftToRead > 0) { memcpy(pData, m_spBuffer.get() + m_readIndex, itemsLeftToRead * sizeof(DataType)); // Bookkeeping m_readIndex += itemsLeftToRead; itemsLeftToRead = 0; } m_freeItems += totalItemsToRead; return totalItemsToRead; } /** * Attempts to write the specified number of items. This is only * guaranteed to write what we have space for. The amount of available * space can be determined by invoking getWriteableItemCount(). * * @return The number of items actually written. */ int write(DataType * pData, int numItems) { int writeableItemCount = getWriteableItemCount(); if (writeableItemCount == 0) return 0; int totalItemsToWrite = std::min(writeableItemCount, numItems); // Note that writeableItemCount will do nothing to help us // determine if we're on the edge of the buffer and need to wrap around. // That's up to us to determine here. int itemsLeftToWrite = totalItemsToWrite; // Note that we're treating m_capacity like an index here for // one-past-the-end. if ((m_writeIndex + itemsLeftToWrite) >= m_capacity) { // We'd exceed the extent of the buffer here if we wrote totalItemsToWrite // samples, so let's do a partial write instead. int itemsAvailableUntilEnd = m_capacity - m_writeIndex; memcpy(m_spBuffer.get() + m_writeIndex, pData, itemsAvailableUntilEnd); // Bookkeeping m_writeIndex = 0; itemsLeftToWrite -= itemsAvailableUntilEnd; pData += itemsAvailableUntilEnd; } if (itemsLeftToWrite > 0) { memcpy(m_spBuffer.get() + m_writeIndex, pData, itemsLeftToWrite * sizeof(DataType)); // Bookkeeping m_writeIndex += itemsLeftToWrite; itemsLeftToWrite = 0; } m_freeItems -= totalItemsToWrite; return totalItemsToWrite; } private: std::unique_ptr<DataType[]> m_spBuffer; //! The data. int m_writeIndex; //!< Where the producer is writing to next. int m_readIndex; //!< Where the consumer is reading from next. const int m_capacity; //!< Total number of frames managed by the ring buffer. std::atomic<int> m_freeItems; //!< Number of frames that are available to be written into. }; |
Hopefully this article has helped you to appreciate the humble ring buffer a little bit more. If ring buffers were new to you before this article, I hope this was a helpful introduction and that you’ll be able to recognize them in the wild when you see them (they’re not always given helpful names like RingBuffer. 🙂 ). The implementation shown here is one of the simplest ones, and just one of many possible ways to do it.
If you find a bug in my code or have any questions or comments, please let me know. If you’ve seen any bizarre ring buffer implementations, tell me about that too. Weird code is always fun to see.
Until next time.